Assignment2.pdf
Question 1: The Instrumental Variable Approach
Step 1) Initialization
First, we define the number of time steps ($N$) along with the coefficients $a_1$ and $a_2$. To introduce noise, we set the standard deviation of white noise corresponding to variances of 4.0 and 9.0. Additionally, we initialize the arrays for the clean system output ($y$), the noisy system output ($y_m$), and the noise vector ($e$).
% Simulation parameters
N = 400; % Number of time steps
a1 = 1.5; % Colored noise coefficient
a2 = -0.7; % Colored noise coefficient
sigma_e = 3; % Standard deviation of white noise (3 for variance = 9.0)
rng(109); %set random seed
% Initialize arrays
y = zeros(N, 1);
ym = zeros(N, 1);
u = 2*(randi([0, 1], N, 1))-1; % Random binary input signal
e = sigma_e * randn(N, 1); % White noise
v = zeros(N, 1); % Initialize colored noiseStep 2) System Simulation
For the simulation, we first apply the clean filter:
$$ y(k) = 1.5 y(k-1) - 0.7 y(k-2) + u(k-1) $$
Then, we create the white noise vector:
$$ e(k) = 2 \cdot \text{randn}(N,1) $$
Finally, the actual system output is simulated:
$$ y_m(k) = y(k) + e(k) $$
We start the simulation from $k=3$ due to dependencies.
Matlab Code
% System simulation (start from k=3 due to dependencies)
for k = 3:N
y(k) = 1.5*y(k-1) - 0.7*y(k-2) + u(k-1);
ym(k) = y(k) + e(k); % Measurement signal
end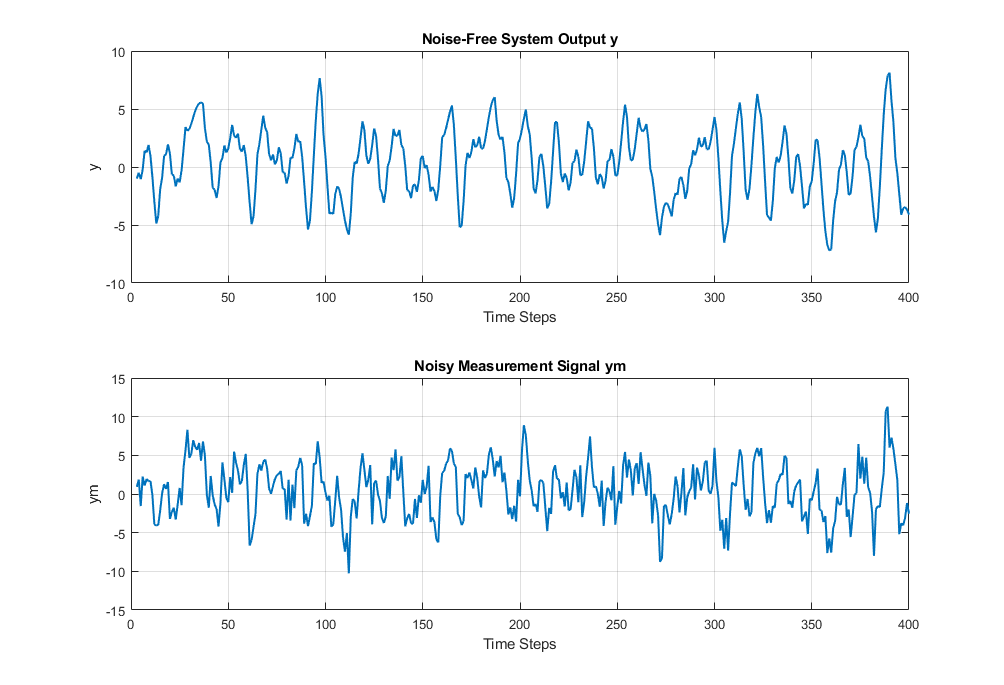
Step 3) Initial Parameters for IV Iterations
To get the first instrumental solution, we compute the Least Squares (LS) estimate:
$$ \theta_{LS} = (\varphi^T \varphi)^{-1} \varphi^T Y $$
where $\varphi$ is the design matrix containing the regressors $[y_m(k-1), y_m(k-2), u(k-1)]$ and $Y$ is the output vector $y_m(3), y_m(4), ... y_m(N)$.
Matlab Code
% Design matrix for noise case
Phi_noise_4 = [ym(2:end-1), ym(1:end-2), u(2:end-1)];
Y_noise_4 = ym(3:end);
% Design matrix for clean case
Phi_clean = [y(2:end-1), y(1:end-2), u(2:end-1)];
Y_clean = y(3:end);From the Matlab output, the LS estimations for clean, noisy (variance $4.0$), and noisy (variance $9.0$) cases are:
| Case | Estimated Parameters from LS |
|---|---|
| Clean Case (True Parameters) | [1.500000, -0.700000, 1.000000] |
| Noise Case (4.0 variance) | [2.077900, -1.357300, 0.373200] |
| Noise Case (9.0 variance) | [2.949300, -2.518900, -0.316400] |
Step 4: Iterative IV Estimation
After obtaining the initial estimates, the Instrumental Variable (IV) method is used to refine them iteratively. The instrumental variable is computed as:
$$ X_i(k) = \theta_{LS}(1) X_i(k-1) - \theta_{LS}(2) X_i(k-2) + \theta_{LS}(3) u(k-1) $$
At each iteration, the instrument matrix $Z$ is formed using lagged values of $X_i(k)$ and the input $u(k)$:
$$ Z = [X_i(k-1), X_i(k-2), u(k-1)] $$
The IV estimate is then updated as:
$$ \theta_{\text{IV}} = (Z^T \Phi)^{-1} (Z^T Y) $$
where $\Phi$ is the regressor matrix. The predicted output is:
$$ y_{\text{pred}} = (\theta_{\text{IV}})^T \Phi_{\text{noise}} $$
The cost function, measuring estimation error, is:
$$ J = \sum (Y - y_{\text{pred}})^2 $$
This iterative process improves parameter estimation by reducing the influence of noise.
Matlab Code
% Simulation parameters
N = 400;
a1 = 1.5;
a2 = -0.7;
sigma_e = 3; % Standard deviation of white noise (3 for variance = 9.0)
rng(109); %set random seed
% Initialize arrays
y = zeros(N, 1);
ym = zeros(N, 1);
u = 2*(randi([0, 1], N, 1))-1; % Random binary input signal
e = sigma_e * randn(N, 1); % White noise
v = zeros(N, 1); % Initialize colored noise
% System simulation (start from k=3 due to dependencies)
for k = 3:N
y(k) = 1.5*y(k-1) - 0.7*y(k-2) + u(k-1);
ym(k) = y(k) + e(k); % Measurement signal
end
% Design matrix for noise case
Phi_noise = [ym(2:end-1), ym(1:end-2), u(2:end-1)];
Y_noise = ym(3:end);
% Design matrix for clean case
Phi_clean = [y(2:end-1), y(1:end-2), u(2:end-1)];
Y_clean = y(3:end);
% Initialize matrices to store the estimated parameters
theta_IV_noise = zeros(3,5);
theta_LS_noise = Phi_noise \ Y_noise;
theta_IV_noise(:,1) = theta_LS_noise.';
cost = zeros(1,6);
J_clean = zeros(1,6);
%% Initialize plot part
t = 3:N;
% no noise
nexttile;
plot(t, y(t), 'LineWidth', 1.5);
title('Noise-Free System Output y');
xlabel('Time Steps');
ylabel('y');
grid on;
% With noise
nexttile;
plot(t, ym(t), 'LineWidth', 1.5);
title('Noisy Measurement Signal ym');
xlabel('Time Steps');
ylabel('ym');
grid on;
% create tiledlayout
figure;
tiledlayout(6,1, 'TileSpacing', 'Compact', 'Padding', 'Compact');
% Run IV iterations
for iter = 1:10
if iter == 1
a1 = theta_LS_noise(1);
a2 = theta_LS_noise(2);
b1 = theta_LS_noise(3);
else
a1 = theta_IV_noise(1,iter-1);
a2 = theta_IV_noise(2,iter-1);
b1 = theta_IV_noise(3,iter-1);
end
Xi = zeros(N, 1); % Initialize instrumental variable
for k = 3:N
Xi(k) = a1 * Xi(k-1) + a2 * Xi(k-2) + b1 * u(k-1);
end
% Construct instrumental variable matrix
Z = [Xi(2:end-1), Xi(1:end-2), u(2:end-1)];
% IV estimation
theta_IV_noise(:,iter) = (Z' * Phi_noise) \ (Z' * Y_noise);
% Predict output
y_pred = Phi_clean * theta_IV_noise(:,iter);
% Compute cost function
cost(iter) = (1/(2*N)) * sum((Y_noise - y_pred).^2);
J_clean(iter) = (1/(2*N)) * sum((Y_clean - y_pred).^2);
% Display results
fprintf('Iteration %d: Parameters: [%f, %f, %f], Cost: %f, J_clean: %f\n', ...
iter, theta_IV_noise(:,iter), cost(iter),J_clean(iter));
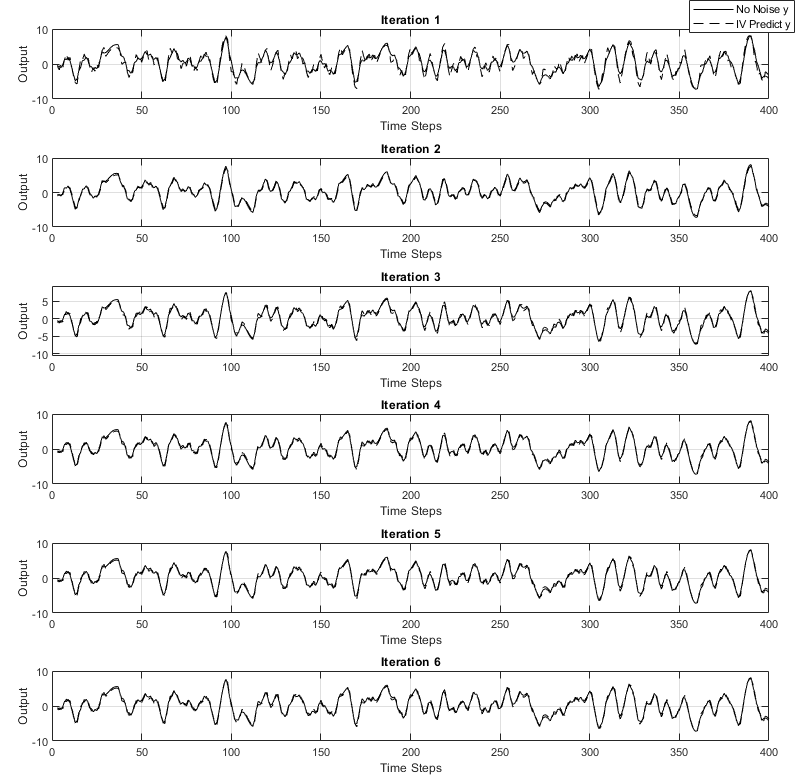
nexttile;
plot(t, y(t), 'k-', 'LineWidth', 0.1);
hold on;
plot(t, y_pred, 'k--', 'LineWidth', 0.1);
title(sprintf('Iteration %d', iter));
xlabel('Time Steps');
ylabel('Output');
legend('No Noise y', sprintf('IV Predict y'), 'Location', 'best');
grid on;
endPlot Variance = 4
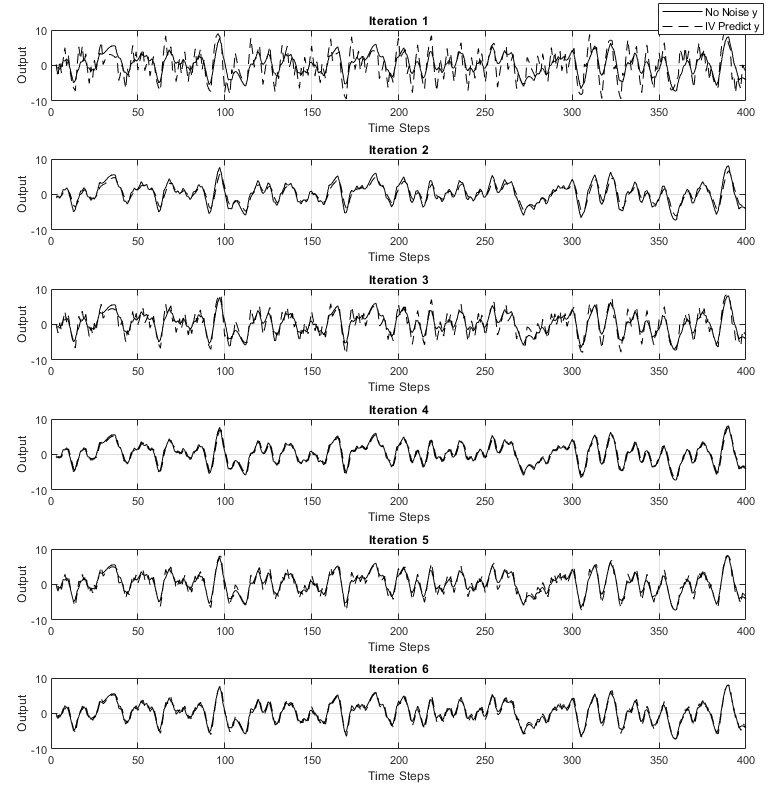
Plot Variance = 9
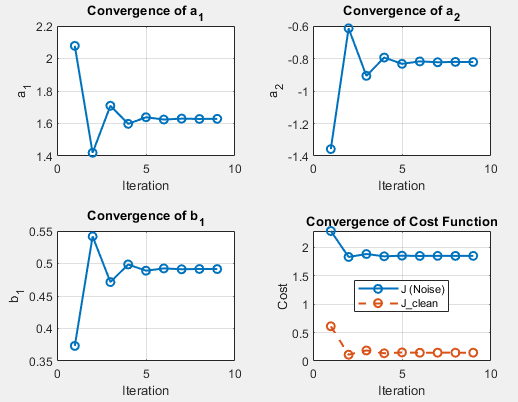
Result
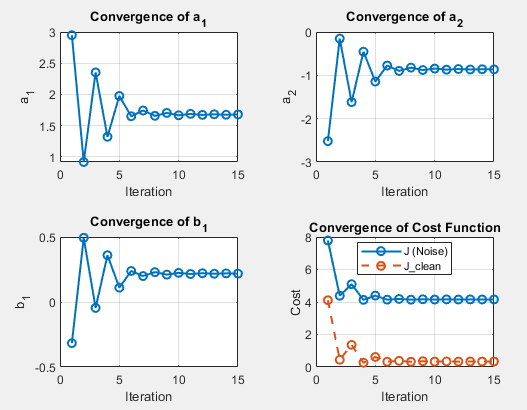
- True Parameter [1.5, -0.7, 1]
Estimated Parameters for Each Iteration (Noise Case: 4.0 Variance)
| Iteration | $a_1$ | $a_2$ | $b_1$ | Cost$J$ | $J_{\text{clean}}$ |
|---|---|---|---|---|---|
| 1 | 2.0779 | -1.3573 | 0.3732 | 2.2825 | 0.6100 |
| 2 | 1.4199 | -0.6144 | 0.5417 | 1.8268 | 0.1108 |
| 3 | 1.7092 | -0.9068 | 0.4714 | 1.8785 | 0.1848 |
| 4 | 1.5979 | -0.7941 | 0.4985 | 1.8377 | 0.1354 |
| 5 | 1.6385 | -0.8328 | 0.4889 | 1.8490 | 0.1501 |
Estimated Parameters for Each Iteration (Noise Case: 9.0 Variance)
| Iteration | $a_1$ | $a_2$ | $b_1$ | Cost$J$ | $J_{\text{clean}}$ |
|---|---|---|---|---|---|
| 1 | 2.9493 | -2.5189 | -0.3164 | 7.7867 | 4.1077 |
| 2 | 0.9185 | -0.1524 | 0.4939 | 4.3865 | 0.4472 |
| 3 | 2.3535 | -1.6182 | -0.0457 | 5.0955 | 1.3665 |
| 4 | 1.3222 | -0.4550 | 0.3596 | 4.1309 | 0.2648 |
| 5 | 1.9760 | -1.1439 | 0.1104 | 4.3928 | 0.6198 |
Conclusion
Instrumental Variable (IV) estimation effectively reduces noise influence, but its performance depends on noise variance. Under moderate noise (4.0 variance), parameters converge smoothly toward the true values, with minor deviations. However, in high noise conditions (9.0 variance), convergence is slower, more erratic, and introduces bias, especially in $b_1$. The cost function decreases in both cases, but higher noise results in a consistently higher cost, indicating less accurate parameter estimates. Overall, IV estimation performs well under controlled noise but struggles with excessive noise.
Question 2) Steepest Descent, LMS and RLS
1. Problem Setup
The given system is represented in the Z-domain as:
$$ \frac{d(z)}{x(z)} = \frac{0.2}{z - 0.8}. $$
Rearranging:
$$ zd(z) - 0.8d(z) = 0.2x(z). $$
Converting to the time domain:
$$ d(n + 1) = 0.2x(n) + 0.8d(n). $$
Assume that the input signal $x(n)$ is white noise with variance $\text{var}[x(n)] = 1$.
The parameter vector to estimate is:
$$ \mathbf{H} = \begin{bmatrix} a \\ b \end{bmatrix}. $$
2. Wiener--Hopf Solution
To find the optimal parameters, we use the Wiener--Hopf equation:
$$ \mathbf{H}_{\text{optimal}} = \mathbf{R}^{-1} \mathbf{p}. $$
where:
- Cross-correlation vector:
$$ \mathbf{p} = \mathbb{E}[ d(n) X(n) ], $$
where $d(n)$ is the desired output, and $X(n)$ is the input vector.
- Autocorrelation matrix:
$$ \mathbf{R} = \mathbb{E} [ X(n) X(n)^T ]. $$
For this system:
- The input signals at time $n$ are $x(n)$ and $d(n)$, so the input vector is:
$$ X(n) = \begin{bmatrix} d(n) \\ x(n) \end{bmatrix}. $$
The cross-correlation vector is:
$$ \mathbf{p} = \mathbb{E} \begin{bmatrix} d(n+1) d(n) \\ d(n+1) x(n) \end{bmatrix}. $$
The autocorrelation matrix is:
$$ \mathbf{R} = \begin{bmatrix} \mathbb{E}[ d^2(n) ] & \mathbb{E}[ d(n)x(n) ] \\[4pt] \mathbb{E}[ x(n)d(n) ] & \mathbb{E}[ x^2(n) ] \end{bmatrix}. $$
With these expressions, we can simulate the system and precompute $\mathbf{p}$ and $\mathbf{R}$ for further calculations.
Below is a straightforward way to carry out the Wiener--Hopf solution in closed form for the system
$$ d(n+1) \;=\; 0.8\,d(n)\;+\;0.2\,x(n), $$
with $x(n)$ white‐noise input of zero mean and variance $\sigma_x^2=1$. We seek the parameter vector
$$ \mathbf{H} = \begin{bmatrix} a\\[3pt] b \end{bmatrix} $$
that minimizes the mean‐square error between the "desired" $d(n+1)$ and the model output $\hat{d}(n+1) = a\,d(n)+b\,x(n)$.
3. Autocorrelation Matrix $\mathbf{R}$
We define the input vector
$$ X(n) \;=\; \begin{bmatrix} d(n)\\[4pt] x(n) \end{bmatrix}. $$
Then the autocorrelation matrix is
$$ \mathbf{R} \;=\; \mathbb{E}\bigl[\,X(n)\,X(n)^\mathsf{T}\bigr] \;=\; \begin{bmatrix} \mathbb{E}[\,d(n)^2\,] & \mathbb{E}[\,d(n)\,x(n)\,]\\[3pt] \mathbb{E}[\,x(n)\,d(n)\,] & \mathbb{E}[\,x(n)^2\,] \end{bmatrix}. $$
Compute $\mathbb{E}[x(n)^2]$.
Since $x(n)$ is white noise with variance 1,$$ \mathbb{E}[\,x(n)^2\,] \;=\; 1. $$
Compute $\mathbb{E}[\,d(n)\,x(n)\,]$.
Because $d(n)$ depends on $x(n-1), x(n-2), \ldots$, and $x(n)$ is uncorrelated with past values of itself, it follows that $d(n)$ is uncorrelated with $x(n)$. Thus,$$ \mathbb{E}[\,d(n)\,x(n)\,] \;=\; 0. $$
Compute $\mathbb{E}[\,d(n)^2\,]$.
Denote $\sigma_d^2 = \mathbb{E}[\,d(n)^2\,]$. From the difference equation,$$ d(n+1) \;=\; 0.8 \, d(n) \;+\; 0.2 \, x(n). $$
In steady state, using the fact that $d(n)$ is uncorrelated with $x(n)$ and
$\sigma_x^2=1$,
$$ \sigma_d^2 \;=\; \mathbb{E}[\,d(n)^2\,] \;=\; 0.8^2\,\sigma_d^2 \;+\; 0.2^2\,\underbrace{\mathbb{E}[\,x(n)^2\,]}_{1}. $$
Hence
$$ \sigma_d^2 \;=\; 0.64\,\sigma_d^2 \;+\; 0.04, \quad\Longrightarrow\quad 0.36\,\sigma_d^2 \;=\; 0.04 \quad\Longrightarrow\quad \sigma_d^2 \;=\; \frac{0.04}{0.36} \;=\; \tfrac{1}{9}. $$
Therefore,
$$ \mathbb{E}[\,d(n)^2\,] \;=\; \frac{1}{9}. $$
Putting it all together,
$$ \mathbf{R} \;=\; \begin{bmatrix} \frac{1}{9} & 0\\[4pt] 0 & 1 \end{bmatrix}. $$
2. Cross‐Correlation Vector $\mathbf{p}$
We need
$$ \mathbf{p} \;=\; \mathbb{E}\bigl[\, d(n+1)\,X(n) \bigr] \;=\; \begin{bmatrix} \mathbb{E}[\,d(n+1)\,d(n)\,]\\[4pt] \mathbb{E}[\,d(n+1)\,x(n)\,] \end{bmatrix}. $$
Use $d(n+1) = 0.8\,d(n) + 0.2\,x(n)$:
First element $\mathbb{E}[\,d(n+1)\,d(n)\,]$:
$$ \mathbb{E}[\,d(n+1)\,d(n)\,] \;=\; \mathbb{E}\bigl[\,(\,0.8\,d(n) + 0.2\,x(n)\,)\,d(n)\bigr] \;=\; 0.8\,\mathbb{E}[\,d(n)^2\,] \;+\; 0.2\,\mathbb{E}[\,x(n)\,d(n)\,]. $$
Since $\mathbb{E}[\,x(n)\,d(n)\,] = 0$, we get
$$ \mathbb{E}[\,d(n+1)\,d(n)\,] \;=\; 0.8 \times \frac{1}{9} \;=\; \frac{0.8}{9} \;=\; \frac{4}{45}. $$
Second element $\mathbb{E}[\,d(n+1)\,x(n)\,]$:
$$ \mathbb{E}[\,d(n+1)\,x(n)\,] \;=\; \mathbb{E}\bigl[\,(0.8\,d(n) + 0.2\,x(n))\,x(n)\bigr] \;=\; 0.8\,\underbrace{\mathbb{E}[\,d(n)\,x(n)\,]}_{0} \;+\; 0.2\,\mathbb{E}[\,x(n)^2\,] \;=\; 0.2 \times 1 \;=\; 0.2. $$
Hence
$$ \mathbf{p} \;=\; \begin{bmatrix} \frac{4}{45}\\[3pt] 0.2 \end{bmatrix}. $$
4. Wiener--Hopf Solution
The optimal parameter vector $\mathbf{H}_{\text{optimal}}$ is given by
$$ \mathbf{H}_{\text{optimal}} \;=\; \mathbf{R}^{-1}\,\mathbf{p}. $$
$$ \mathbf{R} \;=\; \begin{bmatrix} \frac{1}{9} & 0\\[3pt] 0 & 1 \end{bmatrix} \quad\Longrightarrow\quad \mathbf{R}^{-1} \;=\; \begin{bmatrix} 9 & 0\\[3pt] 0 & 1 \end{bmatrix}. $$
Therefore,
$$ \mathbf{H}_{\text{optimal}} \;=\; \begin{bmatrix} 9 & 0\\[3pt] 0 & 1 \end{bmatrix} \begin{bmatrix} \frac{4}{45}\\[3pt] 0.2 \end{bmatrix} \;=\; \begin{bmatrix} 9 \times \frac{4}{45}\\[3pt] 1 \times 0.2 \end{bmatrix} \;=\; \begin{bmatrix} \frac{36}{45}\\[3pt] 0.2 \end{bmatrix} \;=\; \begin{bmatrix} 0.8\\[3pt] 0.2 \end{bmatrix}. $$
Hence the Wiener--Hopf solution for this system is
$$ \boxed{ a \;=\; 0.8, \quad b \;=\; 0.2. } $$
5.Steepest Descent Algorithm
Matlab Code
clear; clc; close all;
%% Generate data
N = 10000; % total samples
x = randn(N,1); % white noise input, var=1
d = zeros(N,1); % desired signal initialization
d(1) = 0; % initial condition
% True system: d(n+1) = 0.8*d(n) + 0.2*x(n)
for k = 1:N-1
d(k+1) = 0.8*d(k) + 0.2*x(k);
end
R = [1/9 0;
0 1 ];
p = [0.8/9; 0.2];
d2 = 1/9;
H_opt = inv(R)*p; % -> [0.8 ; 0.2]
%% Initialize Steepest Descent
alpha = 0.01; % VERY TINY STEP size
H_hat = [0; 0]; % Initial START [a; b]
a_history = zeros(1,N);
b_history = zeros(1,N);
e_array = zeros(1,N); % store instantaneous error
% Store initial values
a_history(1) = H_hat(1);
b_history(1) = H_hat(2);
%% Steepest Descent Loop
for n = 2:N
e_array(n) = d(n) - H_hat(1)*d(n-1) - H_hat(2)*x(n-1);
gradient = -2*p + 2*R*H_hat;
H_hat = H_hat - alpha * gradient;
a_history(n) = H_hat(1);
b_history(n) = H_hat(2);
end
fprintf('Final estimated a = %.4f\n', a_history(end));
fprintf('Final estimated b = %.4f\n', b_history(end));
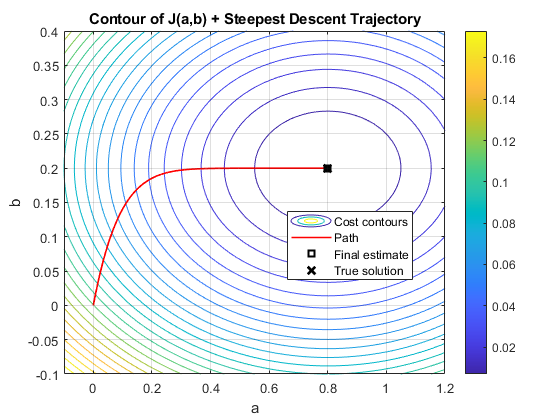
%% Contour Plot of J(a,b) + Parameter Path
na = 60; % grid size for a-axis
nb = 60; % grid size for b-axis
a_range = linspace(-0.1,1.2,na);
b_range = linspace(-0.1,0.4, nb);
J_grid = zeros(na, nb);
% Compute cost function grid
for i = 1:na
for j = 1:nb
A = [a_range(i); b_range(j)];
J_grid(i,j) = d2 - 2*(A.'*p) + (A.'*R*A);
end
end
figure;
contour(a_range, b_range, J_grid.', 25); hold on; grid on; colorbar;
xlabel('a'); ylabel('b');
title('Contour of J(a,b) + Steepest Descent Trajectory');
% Plot the parameter trajectory
plot(a_history, b_history, 'r-','LineWidth',1.2,'MarkerSize',2);
% Mark final estimate
plot(a_history(end), b_history(end), 'ks','MarkerSize',6,'LineWidth',1.5);
% Mark true Wiener solution
plot(H_opt(1), H_opt(2), 'kx','MarkerSize',8,'LineWidth',2);
legend('Cost contours','Path','Final estimate','True solution','Location','best');
hold off;
%% plot a&b est figure
figure;
tiledlayout(2,1, 'TileSpacing', 'Compact', 'Padding', 'Compact');
% a_est plot
nexttile;
plot(a_history,'-','MarkerSize',2); hold on;
yline(H_opt(1),'r--','LineWidth',1.5);
xlabel('Iteration'); ylabel('a_{est}');
legend('a_{est}','true a=0.8','Location','best');
title('a_{est} vs. Iteration (Full)');
grid on;
% b_est plot
nexttile;
plot(b_history,'-','MarkerSize',2); hold on;
yline(H_opt(2),'r--','LineWidth',1.5);
xlabel('Iteration'); ylabel('b_{est}');
legend('b_{est}','true b=0.2','Location','best');
title('b_{est} vs. Iteration (Full)');
grid on;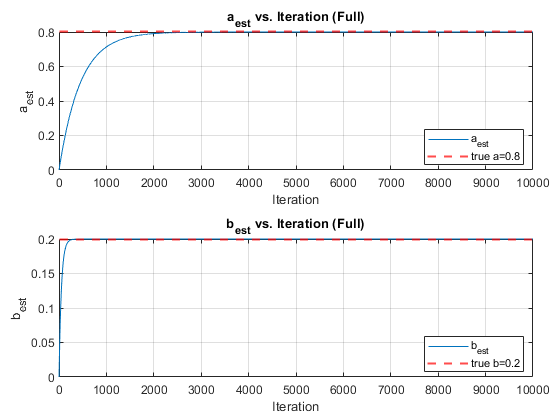
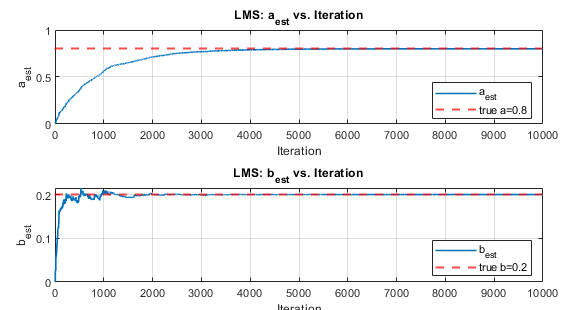
6.LMS Algorithm
The parameters are updated using the Least Mean Squares (LMS) rule:
$$ e(n) = d(n) - [a_{\text{est}} d(n-1) + b_{\text{est}} x(n-1)] $$
$$ H_{\text{hat}} = H_{\text{hat}} + \mu \cdot e(n) \cdot \begin{bmatrix} d(n-1) \\ x(n-1) \end{bmatrix} $$
for n = 2:N
% Input vector at time n (one-step-behind signals)
Xn = [ d(n-1); x(n-1) ];
% Predicted output
y_hat = H_hat.' * Xn; % = a_est*d(n-1) + b_est*x(n-1)
% Error
e_array(n) = d(n) - y_hat;
% LMS parameter update
H_hat = H_hat + mu * e_array(n) * Xn;
% Store
a_history(n) = H_hat(1);
b_history(n) = H_hat(2);
endPlots
We will plot the following:
- Parameter Trajectory: $(a_{\text{est}}, b_{\text{est}})$
Cost Surface Contour:
- The contour $J(a,b)$ derived from the Wiener formula.
- This allows visualization of how LMS moves within the cost surface.
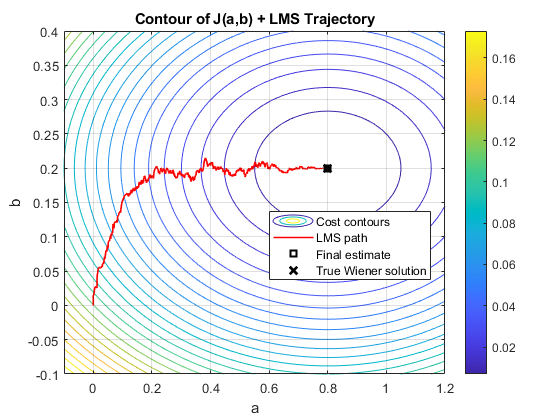
7.Standard Recursive Least Squares Algorithm(λ = 1.0)
We use the classic RLS recursion:
Input Vector:
$$ X(n) = \begin{bmatrix} d(n-1) \\ x(n-1) \end{bmatrix} $$
Predicted Output:
$$ \hat{y}(n) = H_{\text{hat}}(n-1)^T X(n) $$
Error Calculation:
$$ e(n) = d(n) - \hat{y}(n) $$
Gain Vector:
$$ K(n) = \frac{P(n-1) X(n)}{\lambda + X(n)^T P(n-1) X(n)} $$
Parameter Update:
$$ H_{\text{hat}}(n) = H_{\text{hat}}(n-1) + K(n) e(n) $$
Covariance Matrix Update:
$$ P(n) = \frac{P(n-1) - K(n) X(n)^T P(n-1)}{\lambda} $$
%% 4. RLS LOOP
for n = 2:N
% 1) Current regressor: X(n) = [ d(n-1); x(n-1) ]
Xn = [ d(n-1); x(n-1) ];
% 2) Predicted output
y_hat = H_hat.' * Xn;
% 3) Error
e_array(n) = d(n) - y_hat;
% 4) Gain vector
denom = lambda + Xn.' * P * Xn; % scalar
K = (P * Xn) / denom;
% 5) Parameter update
H_hat = H_hat + K * e_array(n);
% 6) Covariance update
P = (P - K * (Xn.' * P)) / lambda;
% Store results
a_history(n) = H_hat(1);
b_history(n) = H_hat(2);
endPlots
We visualize:
- The parameter trajectory $(a_{\text{est}}, b_{\text{est}})$.
- The cost surface contour $J(a, b)$ from the Wiener solution to compare the behavior of the RLS algorithm.
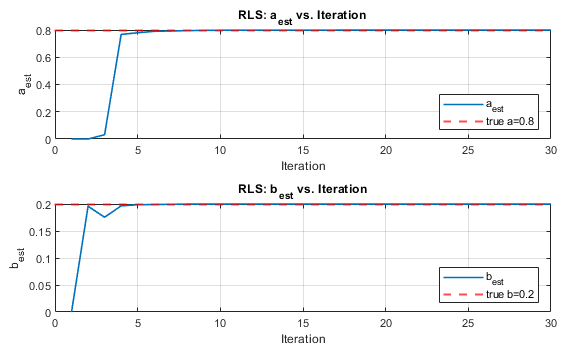
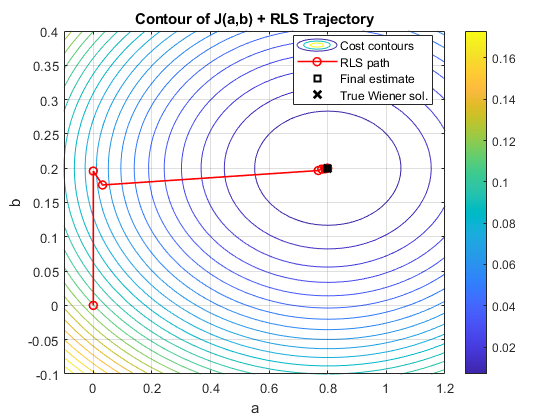
8.Comment on the Difference
SGD (Stochastic Gradient Descent)
- Performance: The core idea of SGD is to adjust the parameters by calculating the gradient of the error (that is, the direction in which the error changes the fastest), so that the parameters are updated in the direction of reducing the error. This method is very efficient in most cases, especially when the amount of data is large.
- Complexity: The calculation of SGD mainly relies on the multiplication of matrices and vectors. If the data scale is small (such as low dimensions of parameters and data), the amount of calculation is not large; but if the data scale is large (such as high-dimensional data or large-scale matrices), the calculation and storage will become very laborious. Therefore, although SGD itself is not complex, calculation and storage may become a bottleneck when processing large-scale data, especially when the signal is unstable (such as the data distribution changes over time).
- Implementation issues: SGD needs to store some data in advance (such as vector p and matrix R), which is feasible when the signal is stable. But if the signal is unstable (such as the data distribution changes over time) or the system characteristics change dynamically, the pre-stored data is no longer applicable.
LMS (Least Mean Squares)
- Performance: LMS is a simpler gradient descent method, especially suitable for situations where data cannot be stored in advance (such as unstable signals or high-dimensional data). It does not directly calculate the entire error surface, but updates the parameters by estimating the current error, so it is called a "dirty gradient".
- Complexity: LMS is very simple to calculate because it only uses a fixed learning rate to update the parameters, avoiding complex matrix operations. This makes it very efficient and suitable for real-time processing.
- Implementation issues: The main problem with LMS is that it is very sensitive to the choice of learning rate. If the learning rate is set too small, the convergence speed will be slow; if it is set too large, it may cause parameter oscillation or even failure to converge.
RLS (Recursive Least Squares)
- Performance: RLS is a very fast algorithm because it uses the inverse information of the autocorrelation matrix to adjust the parameters more accurately. It usually converges much faster than LMS and SGD.
- Complexity: The disadvantage of RLS is that it has a high computational complexity because it requires matrix operations, such as matrix inversion. These operations require high computing resources, especially when the data dimension is large.
- Implementation issues: Due to the high computational complexity of RLS, it is difficult to implement on hardware with limited resources. In addition, RLS has high requirements for numerical stability, and matrix inversion may cause numerical instability (such as "numerical expansion" phenomenon), which will affect the performance of the algorithm.
Question 3
a)
Matlab Code
% a) Recursive Least Squares (RLS) for system identification
clear; clc; close all;
rng(109);
N = 400;
sigma_e = 2; % Standard deviation of noise
lambda_values = [1.0, 0.95]; % Forgetting factors
theta_true = [1.5; -0.7; 1.0];
y = zeros(N,1);
u = 2 * (rand(N,1) > 0.5) - 1; % Random binary input signal (±1)
% Simulate the system
for k = 3:N
e = sigma_e * randn;
y(k) = 1.5*y(k-1) - 0.7*y(k-2) + u(k-1) + e;
end
% Function to perform RLS estimation
for lambda = lambda_values
theta_est = zeros(3, N);
P = 1000 * eye(3);
trace_P = zeros(N,1);
for k = 3:N
phi = [y(k-1); y(k-2); u(k-1)]; % Regression vector
K = P * phi / (lambda + phi' * P * phi); % Gain
error = y(k) - phi' * theta_est(:, k-1); % Prediction error
theta_est(:, k) = theta_est(:, k-1) + K * error;
P = (P - (K * phi') * P) / lambda; % Update covariance
trace_P(k) = trace(P); % Store trace
end
figure;
subplot(2,1,1);
plot(theta_est(1,:), 'r', 'LineWidth', 1.5); hold on;
plot(theta_est(2,:), 'g', 'LineWidth', 1.5);
plot(theta_est(3,:), 'b', 'LineWidth', 1.5);
yline(1.5, 'r--', 'True \theta_1');
yline(-0.7, 'g--', 'True \theta_2');
yline(1.0, 'b--', 'True \theta_3');
xlabel('Time Step');
ylabel('\theta Estimates');
legend('\theta_1', '\theta_2', '\theta_3', 'Location', 'best');
title(['Parameter Estimates (\lambda = ', num2str(lambda), ')']);
grid on;
subplot(2,1,2);
plot(trace_P, 'k', 'LineWidth', 1.5);
xlabel('Time Step');
ylabel('Trace(P)');
title(['Trace of Covariance Matrix (\lambda = ', num2str(lambda), ')']);
grid on;
end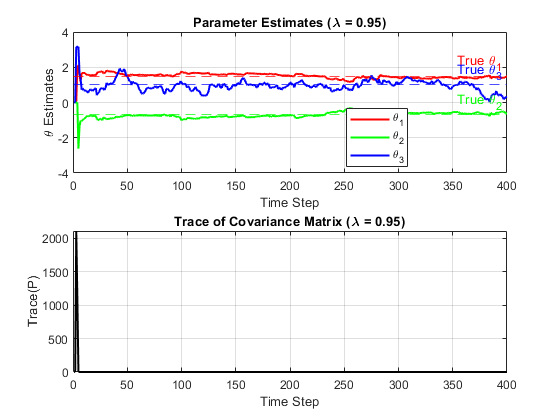
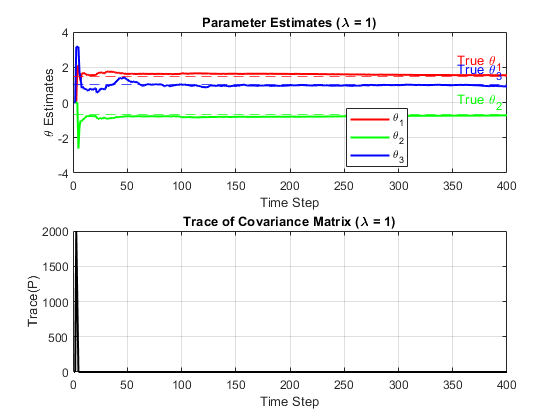
Is there a difference?
Yes!When comparing the results of $\lambda = 1.0$ and $\lambda = 0.95$, we find that they have significant differences in parameter stability and covariance matrix behavior. When $\lambda = 1.0$, the parameter estimates quickly stabilize and closely track the true values, with little fluctuation, and the trace of the covariance matrix also converges smoothly, indicating that the estimation process is stable and consistent. When $\lambda = 0.95$, the parameter estimates show more fluctuations because the algorithm pays more attention to recent data and is more sensitive to new observations. The trace of the covariance matrix also fluctuates more, reflecting the increased uncertainty in the estimation process.
b)
%% MATLAB Code for Part (b): RLS with Changing Input Signal
clear all; close all; clc;
rng(109);
N = 400;
sigma_e = 2;
y = zeros(N,1);
u = zeros(N,1);
%% Generate the Input Signal u(k)
% For k = 1 to 99, u(k) is random binary: +1 or -1
u(1:99) = 2*(rand(99,1) > 0.5) - 1;
% For k = 100 to 300, set u(k) = +1.0
u(100:300) = 0;
% For k = 301 to 400, u(k) returns to random binary: +1 or -1
u(301:400) = 2*(rand(100,1) > 0.5) - 1;
%% Simulate the System
y(1:2) = 0;
for k = 3:N
e = sigma_e * randn;
y(k) = 1.5*y(k-1) - 0.7*y(k-2) + u(k-1) + e;
end
%% RLS Algorithm Setup
lambda = 0.95;
n_params = 3;
theta_est = zeros(n_params, N);
P = 1000 * eye(n_params);
traceP = zeros(N,1);
%% Run the RLS Algorithm
for k = 3:N
phi = [y(k-1); y(k-2); u(k-1)];
K = P * phi / (lambda + phi' * P * phi);
error = y(k) - phi' * theta_est(:, k-1);
theta_est(:, k) = theta_est(:, k-1) + K * error;
P = (P - K * phi' * P) / lambda;
traceP(k) = trace(P);
end
time = 1:N; % Time vector
figure;
subplot(2,1,1);
plot(time, theta_est(1,:), 'r-', 'LineWidth', 2); hold on;
plot(time, theta_est(2,:), 'b-', 'LineWidth', 2);
plot(time, theta_est(3,:), 'g-', 'LineWidth', 2);
xlabel('Time Step k');
ylabel('Parameter Estimates');
legend('\theta_1','\theta_2','\theta_3','Location','Best');
title('RLS Parameter Estimates with \lambda = 0.95');
grid on;
subplot(2,1,2);
plot(time, traceP, 'k-', 'LineWidth', 2);
xlabel('Time Step k');
ylabel('Trace of Covariance Matrix P');
title('Trace of Covariance Matrix P over Time');
grid on;
fprintf('Final parameter estimates:\n');
fprintf('theta1 = %.4f\n', theta_est(1,end));
fprintf('theta2 = %.4f\n', theta_est(2,end));
fprintf('theta3 = %.4f\n', theta_est(3,end));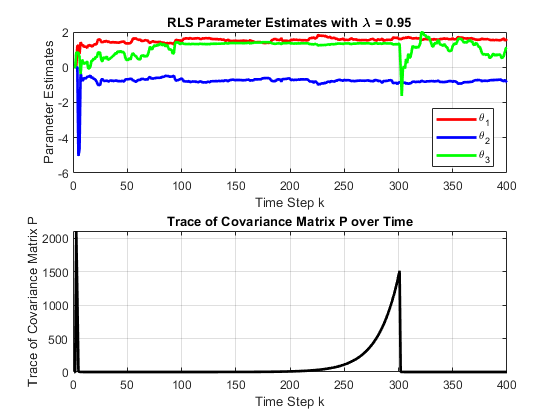
The RLS algorithm shows fast convergence, quickly stabilizing the parameter estimates ($\theta_1$, $\theta_2$, and $\theta_3$) . From chosen forgetting factor $\lambda = 0.95$. Between $k = 100$ and $k = 300$. The parameters remain stable as the input signal $u(k)$ is unchanged. However, at $k = 300$, when the input switches back to a binary signal, $\theta_3$ experiences significant fluctuations, indicating its higher sensitivity to input variations. The trace of the covariance matrix $P$ rises sharply between $k = 200$ and $k = 300$, reflecting increased uncertainty, but it starts decreasing after $k = 300$. It is showing that the algorithm is adapting to the new input conditions.
c)
%% MATLAB Code for Part (c): Time-Varying Parameters
clear all; close all; clc;
rng(109);
N = 400; % Total number of data points
sigma_e = 2; % Standard deviation of noise (sqrt(variance)=2)
y = zeros(N,1); % Pre-allocate output vector
u = zeros(N,1); % Pre-allocate input vector
%% Generate the Input Signal u(k)
% For k = 1 to 99, u(k) is random binary: +1 or -1
u(1:99) = 2*(rand(99,1) > 0.5) - 1;
% For k = 100 to 300, set u(k) = +1.0
u(100:300) = 0;
% For k = 301 to 400, u(k) returns to random binary: +1 or -1
u(301:400) = 2*(rand(100,1) > 0.5) - 1;
%% Simulate the Time-Varying System
y(1:2) = 0;
for k = 3:N
e = sigma_e * randn;
if k < 250
% Before time step 250: original parameters
y(k) = 1.5*y(k-1) - 0.7*y(k-2) + u(k-1) + e;
else
% At and after time step 250: changed parameters
y(k) = 1.7*y(k-1) - 0.9*y(k-2) + 5*u(k-1) + e;
end
end
%% RLS Algorithm Setup
lambda = 0.95;
n_params = 3;
theta_est = zeros(n_params, N);
P = 1000 * eye(n_params);
traceP = zeros(N,1);
%% Run the RLS Algorithm
for k = 3:N
phi = [y(k-1); y(k-2); u(k-1)];
K = P * phi / (lambda + phi' * P * phi);
error = y(k) - phi' * theta_est(:, k-1);
theta_est(:, k) = theta_est(:, k-1) + K * error;
P = (P - K * phi' * P) / lambda;
traceP(k) = trace(P);
end
%% Plot the Results
time = 1:N; % Time vector
figure;
subplot(2,1,1);
plot(time, theta_est(1,:), 'r-', 'LineWidth', 2); hold on;
plot(time, theta_est(2,:), 'b-', 'LineWidth', 2);
plot(time, theta_est(3,:), 'g-', 'LineWidth', 2);
xlabel('Time Step k');
ylabel('Parameter Estimates');
legend('\theta_1','\theta_2','\theta_3','Location','Best');
title('RLS Parameter Estimates with a Parameter Change at k = 250');
grid on;
subplot(2,1,2);
plot(time, traceP, 'k-', 'LineWidth', 2);
xlabel('Time Step k');
ylabel('Trace(P)');
title('Trace of the Covariance Matrix P over Time');
grid on;
fprintf('Final parameter estimates:\n');
fprintf('theta1 = %.4f\n', theta_est(1,end));
fprintf('theta2 = %.4f\n', theta_est(2,end));
fprintf('theta3 = %.4f\n', theta_est(3,end));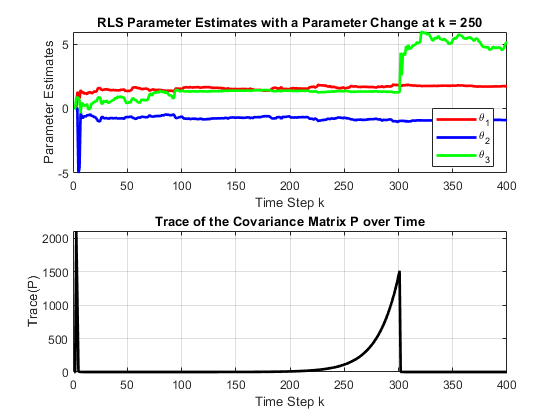
Observations on the Results:
Parameter Estimates Before k = 250 :
- The estimated parameters ($\theta_1$, $\theta_2$, and $\theta_3$) are stable and remain relatively constant, showing that the RLS algorithm has successfully converged to an initial solution.
$k$ = 250 :
- At $k$ = 250, the true system parameters were modified ($\theta_1$, $\theta_2$, and $\theta_3$). However, the estimated parameters take some time to reflect this change.
Excitation at $k$ = 300
- At $k = 300$ the input signal $u(k)$ switches back to a random binary signal, introducing significant variations in the estimated parameters.
- $\theta_3$ (green) is particularly affected, experiencing a sharp increase, indicating that it is more sensitive to changes in the input signal.
- This suggests that $\theta_3$ is closely linked to the input excitation and that the sudden change in signal structure strongly influences it.
Covariance Matrix Trace Behavior:
- The trace of the covariance matrix $P$ increases gradually from $k = 250$ and peaks around $k = 300$, which indicates a period of high uncertainty.
- Once the new parameter values are learned and the algorithm adapts, the trace begins to decrease, showing that confidence in the estimates is being restored.
Key Information:
- The RLS algorithm successfully tracks parameter changes but takes time to adapt.
- The impact of the signal excitation at $k = 300$ is significant, especially for $\theta_3$.
- The covariance trace confirms increased uncertainty after parameter and input changes but stabilizes as the algorithm adapts.
One comment
看不懂,但高级!好!ദ്ദി˶•̀֊•́)✧