Loading... [SYSC 5108 W25 Assignment 3.pdf](https://wwang7.synology.me:8031/usr/uploads/2025/03/936283889.pdf) # SYSC 5108 W25 ssignment 3 William Wang 101191168 ## Q1 From the Beta–Binomial conjugacy principle, a uniform $\theta \sim \text{Beta}(1,1)$ prior combined with the Binomial likelihood (with $x$ successes out of $n$ yields a posterior distribution $$ p(\theta \mid x) = \text{Beta}\bigl(x + 1,\; n - x + 1\bigr). $$ ## Q2 ### (a) Weighted sum = $0.20 \cdot 1 + (-0.10) \cdot 0.2 + 0.25 \cdot 0.5 + 0.05 \cdot 0.7 = 0.34$ ### (b) Threshold ($\theta = 1$) output = $$ \begin{cases} 1 & \text{if } 0.34 \ge 1 \\ 0 & \text{otherwise} \end{cases} $$ $$ $$ So output = 0. ## (c) Logistic ($\varphi$) output = $$ \frac{1}{1 + e^{-0.34}} \approx 0.58. $$ ## (d) ReLU output = $\max(0,\,0.34) = 0.34.$ ## Q3 ### (a) Logistic (sigmoid) activation - **Neuron 3** $a_3 = \sigma(z_3)= \tfrac{1}{1 + e^{-(1.0 \times 0.7) + (0.6 \times 0.3) + 0.1 = 0.7 + 0.18 + 0.1}} = \tfrac{1}{1 + e^{-0.98}} \approx 0.73.$ - **Neuron 4** $a_4 = \sigma(z_4)= \tfrac{1}{1 + e^{-(0.9 \times 0.7) + (-0.8 \times 0.3) + 0.5 = 0.63 - 0.24 + 0.5 }} = \tfrac{1}{1 + e^{-0.89}} \approx 0.71.$ - **Neuron 5** $a_5 = \sigma(z_5) = \tfrac{1}{1 + e^{-(0.3 \times 0.73) + (0.2 \times 0.71) + 0.9 \approx 0.219 + 0.142 + 0.9}} = \tfrac{1}{1 + e^{-1.261}} \approx 0.78.$ **Neuron 5’s output $\approx 0.78$.** ### (b) ReLU activation - **Neuron 3** $a_3 = \max(0,\,0.98) = 0.98.$ - **Neuron 4** $a_4 = \max(0,\,0.89) = 0.89.$ - **Neuron 5** $a_5 = \max(0,\,1.372) = 1.372.$ Hence, **Neuron 5’s output $\approx 1.37$.** ### (c) Filling in the network diagram (ReLU case) - **Weights and biases** : - $w_{3,1} = 1.0,\; w_{3,2} = 0.6,\; b_3 = 0.1$ - $w_{4,1} = 0.9,\; w_{4,2} = -0.8,\; b_4 = 0.5$ - $w_{5,3} = 0.3,\; w_{5,4} = 0.2,\; b_5 = 0.9$ - **Neuron 3** - Weighted sum: $z_3 = 1.0 \times 0.7 + 0.6 \times 0.3 + 0.1 = 0.98$ - Activation: $a_3 = \mathrm{ReLU}(0.98) = 0.98$ - **Neuron 4** - Weighted sum: $z_4 = 0.9 \times 0.7 + (-0.8) \times 0.3 + 0.5 = 0.89$ - Activation: $a_4 = \mathrm{ReLU}(0.89) = 0.89$ - **Neuron 5** - Weighted sum: $z_5 = 0.3 \times a_3 + 0.2 \times a_4 + 0.9 = 1.372$ - Activation: $a_5 = \mathrm{ReLU}(1.372) = 1.372$ 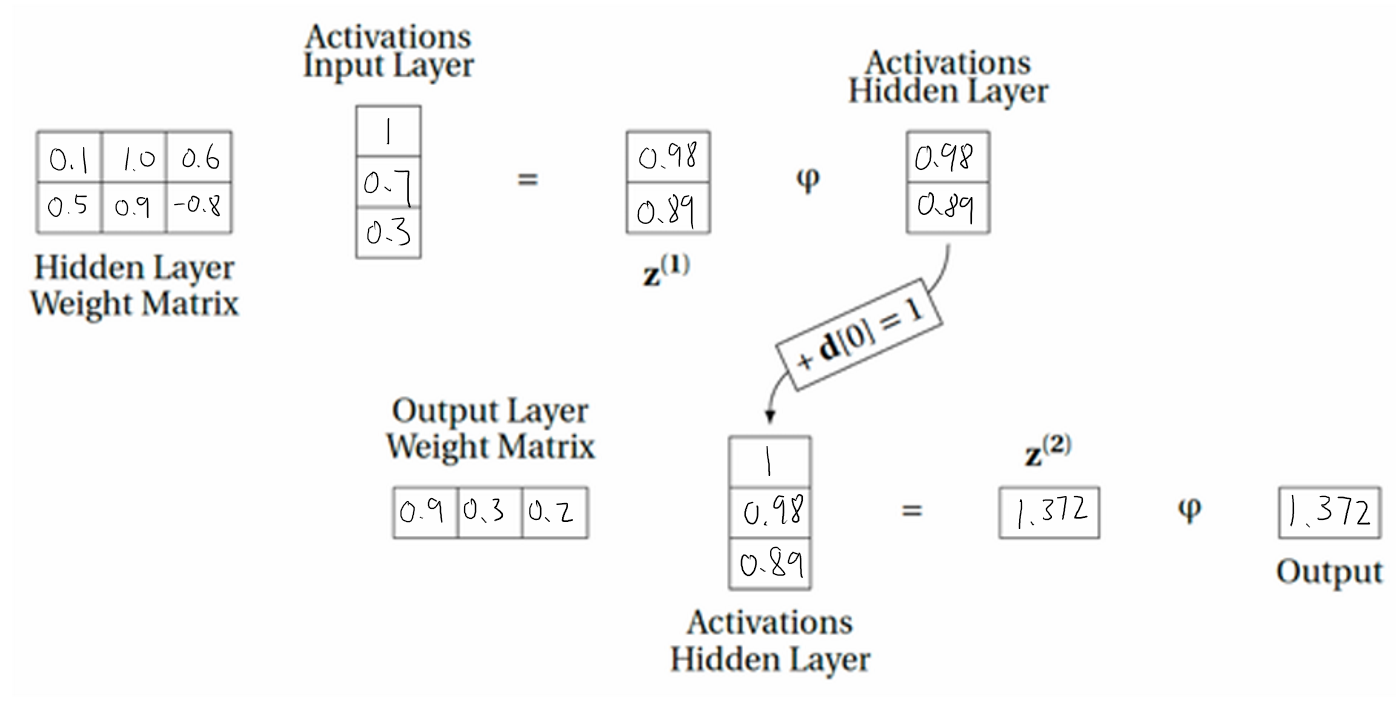 ## Q4 ### (a) Network Output $$ \begin{aligned} &\text{Hidden neurons:} \\ &a_2 = \max(0, 0.2 \times 0.5) = 0.1, \\ &a_3 = \max(0, 0.3 \times 0.5) = 0.15, \\ &a_4 = \max(0, 0.4 \times 0.5) = 0.2. \\ &\text{Output neuron:} \\ &y = a_5 = \max\bigl(0, (0.5 \times 0.1) + (0.6 \times 0.15) + (0.7 \times 0.2)\bigr) \\ &\quad = \max(0, 0.05 + 0.09 + 0.14) \\ &\quad = \max(0, 0.28) \\ &\quad = 0.28. \end{aligned} $$ ### (b) Error Values ($\delta$) for Each Processing Neuron $$ E = \frac{1}{2} (t - y)^2 = \frac{1}{2} (0.9 - 0.28)^2 = \frac{1}{2} (0.62)^2 = 0.1922. $$ ### (c) Gradients of the Error w.r.t. Each Weight $$ \delta_5 = (y - t)\cdot \mathbf{1}_{z_5>0} = (0.28 - 0.9)\times 1 = -0.62. $$ For hidden neurons $i \in \{2,3,4\}$: $$ \delta_i = \delta_5 \times w_{5,i}, $$ thus $$ \delta_2 = -0.62 \times 0.5 = -0.31, \quad \delta_3 = -0.62 \times 0.6 = -0.372, \quad \delta_4 = -0.62 \times 0.7 = -0.434. $$ ### (d) Weight Updates with $\alpha=0.1$ The gradient formulas are: $$ \frac{\partial E}{\partial w_{5,i}} = \delta_5\,a_i, \quad \frac{\partial E}{\partial w_{i,1}} = \delta_i \, x. $$ Output layer: $$ \begin{aligned} \frac{\partial E}{\partial w_{5,2}} &= \delta_5 \, a_2 = (-0.62)\times0.1 = -0.062,\\ \frac{\partial E}{\partial w_{5,3}} &= (-0.62)\times0.15 = -0.093,\\ \frac{\partial E}{\partial w_{5,4}} &= (-0.62)\times0.2 = -0.124. \end{aligned} $$ Hidden layer: $$ \begin{aligned} \frac{\partial E}{\partial w_{2,1}} &= \delta_2 \times x = (-0.31)\times0.5 = -0.155,\\ \frac{\partial E}{\partial w_{3,1}} &= (-0.372)\times0.5 = -0.186,\\ \frac{\partial E}{\partial w_{4,1}} &= (-0.434)\times0.5 = -0.217. \end{aligned} $$ ### (e) Recalculation of the Error with Updated Weights With learning rate $\alpha=0.1$, each weight update is $$ w \leftarrow w - \alpha \,\frac{\partial E}{\partial w}. $$ Output layer: $$ \begin{aligned} w_{5,2}^{\text{new}} &= 0.5 - 0.1\times(-0.062) = 0.5 + 0.0062 = 0.5062,\\ w_{5,3}^{\text{new}} &= 0.6 - 0.1\times(-0.093) = 0.6 + 0.0093 = 0.6093,\\ w_{5,4}^{\text{new}} &= 0.7 - 0.1\times(-0.124) = 0.7 + 0.0124 = 0.7124. \end{aligned} $$ Hidden layer: $$ \begin{aligned} w_{2,1}^{\text{new}} &= 0.2 - 0.1\times(-0.155) = 0.2 + 0.0155 = 0.2155,\\ w_{3,1}^{\text{new}} &= 0.3 - 0.1\times(-0.186) = 0.3 + 0.0186 = 0.3186,\\ w_{4,1}^{\text{new}} &= 0.4 - 0.1\times(-0.217) = 0.4 + 0.0217 = 0.4217. \end{aligned} $$ Checking the New Error(Forward Pass with Updated Weights): $$ \begin{aligned} a_2' &= \max(0, 0.2155\times0.5) = 0.10775,\\ a_3' &= \max(0, 0.3186\times0.5) = 0.1593,\\ a_4' &= \max(0, 0.4217\times0.5) = 0.21085,\\ y' &= a_5' = \max\bigl(0, 0.5062\times0.10775 + 0.6093\times0.1593 + 0.7124\times0.21085\bigr) \approx 0.302. \end{aligned} $$ $$ E' = \frac{1}{2} (t - y')^2 = \frac{1}{2} (0.9 - 0.302)^2 = 0.1788 < 0.1922. $$ Thus, the error has decreased, indicating successful training for this step. ## Q5 ### a) What value will this network output? Define the input: $$ [1, 2, 3, 4, 5, 6] $$ The first layer is a convolution with a window size of 3 and stride 1. The filter has weights: $w_1 = 1, \quad w_2 = 1, \quad w_3 = 1 $ and a bias: $w_0 = 0.75$ Since this is a simple sum followed by a bias addition, we slide the window over the input, computing the convolution at each position. For the first position using \([1,2,3]\): $$ z_1 = (1 + 2 + 3) + 0.75 = 6.75 $$ $$ a_1 = \max(0, 6.75) = 6.75 $$ For the second position using \([2,3,4]\): $$ z_2 = (2 + 3 + 4) + 0.75 = 9.75 $$ $$ a_2 = \max(0, 9.75) = 9.75 $$ For the third position using \([3,4,5]\): $$ z_3 = (3 + 4 + 5) + 0.75 = 12.75 $$ $$ a_3 = \max(0, 12.75) = 12.75 $$ For the fourth position using \([4,5,6]\): $$ z_4 = (4 + 5 + 6) + 0.75 = 15.75 $$ $$ a_4 = \max(0, 15.75) = 15.75 $$ At this point, the feature map after the convolutional layer is: $$ [6.75, 9.75, 12.75, 15.75] $$ Next, we apply max pooling with kernel size 2 and stride 2. The first pooling window takes: $$ \max(6.75, 9.75) = 9.75 $$ The second pooling window takes: $$ \max(12.75, 15.75) = 15.75 $$ So, after max pooling, the output is: $$ [9.75, 15.75] $$ Now, these two values go into the fully connected layer. There is only one neuron, which has: - Bias: $w_4 = 1 $ - Weights: $w_5 = 0.2, \quad w_6 = 0.5$ The neuron computes: $$ z_7 = w_4 + w_5 \cdot 9.75 + w_6 \cdot 15.75 $$ Substituting the values: $$ z_7 = 1 + (0.2 \times 9.75) + (0.5 \times 15.75) $$ Calculating step-by-step: $$ 0.2 \times 9.75 = 1.95 $$ $$ 0.5 \times 15.75 = 7.875 $$ $$ z_7 = 1 + 1.95 + 7.875 = 10.825 $$ Applying ReLU: $$ \max(0, 10.825) = 10.825 $$ So, the final output of the network is: $$ \boxed{10.825} $$ ### b) calculate the 𝛿 for each neuron in the network. The loss function is mean squared error: $$ E = \frac{1}{2} (t - y)^2 $$ Taking the derivative with respect to \( N_7 \): $$ \delta_7 = \frac{\partial E}{\partial N_7} = (y - t) $$ Substituting values: $$ \delta_7 = 10.825 - 1 = 9.825 $$ $$ \delta_5 = \delta_7 \times w_5 = 9.825 \times 0.2 = 1.965 $$ $$ \delta_6 = \delta_7 \times w_6 = 9.825 \times 0.5 = 4.9125 $$ Neuron 5 pools $ (N_1, N_2) $, where the max was $ N_2 = 9.75 $. So only $ \delta_2 $ receives $ \delta_5 $, while $ \delta_1 = 0 $. $$ \delta_2 = \delta_5 = 1.965, \quad \delta_1 = 0 $$ Neuron 6 pools $ (N_3, N_4) $, where the max was $ N_4 = 15.75 $. So only$ \delta_4 $ receives $ \delta_6 $, while $ \delta_3 = 0 $. $$ \delta_4 = \delta_6 = 4.9125, \quad \delta_3 = 0 $$ Results: $$ \delta_1 = 0 $$ $$ \delta_2 = 1.965 $$ $$ \delta_3 = 0 $$ $$ \delta_4 = 4.9125 $$ $$ \delta_5 = 1.965 $$ $$ \delta_6 = 4.9125 $$ $$ \delta_7 = 9.825 $$ ### c) $$ N_2 = \text{ReLU}(w_0 + w_1\cdot2 + w_2\cdot3 + w_3\cdot4). $$ Taking partial derivatives: $$ \frac{\partial N_2}{\partial w_0} = 1, \quad \frac{\partial N_2}{\partial w_1} = 2, \quad \frac{\partial N_2}{\partial w_2} = 3, \quad \frac{\partial N_2}{\partial w_3} = 4. $$ Since \(N_2 > 0\), the ReLU derivative is 1, so the gradient contribution from \( N_2 \) is: $$ \frac{\partial E}{\partial w_0} \Big|_{N_2} = \delta_2 \times 1 = 1.965, $$ $$ \frac{\partial E}{\partial w_1} \Big|_{N_2} = \delta_2 \times 2 = 3.93, $$ $$ \frac{\partial E}{\partial w_2} \Big|_{N_2} = \delta_2 \times 3 = 5.895, $$ $$ \frac{\partial E}{\partial w_3} \Big|_{N_2} = \delta_2 \times 4 = 7.86. $$ Since \( N_4 \) is computed as: $$ N_4 = \text{ReLU}(w_0 + w_1\cdot4 + w_2\cdot5 + w_3\cdot6). $$ Taking partial derivatives: $$ \frac{\partial N_4}{\partial w_0} = 1, \quad \frac{\partial N_4}{\partial w_1} = 4, \quad \frac{\partial N_4}{\partial w_2} = 5, \quad \frac{\partial N_4}{\partial w_3} = 6. $$ Since \(N_4 > 0\), the ReLU derivative is 1, so the gradient contribution from \( N_4 \) is: $$ \frac{\partial E}{\partial w_0} \Big|_{N_4} = \delta_4 \times 1 = 4.9125, $$ $$ \frac{\partial E}{\partial w_1} \Big|_{N_4} = \delta_4 \times 4 = 19.65, $$ $$ \frac{\partial E}{\partial w_2} \Big|_{N_4} = \delta_4 \times 5 = 24.5625, $$ $$ \frac{\partial E}{\partial w_3} \Big|_{N_4} = \delta_4 \times 6 = 29.475. $$ Since \(w_j\) appears in both \(N_2\) and \(N_4\), the total gradient for each weight is the sum of both contributions: $$ \frac{\partial E}{\partial w_0} = 1.965 + 4.9125 = 6.8775, $$ $$ \frac{\partial E}{\partial w_1} = 3.93 + 19.65 = 23.58, $$ $$ \frac{\partial E}{\partial w_2} = 5.895 + 24.5625 = 30.4575, $$ $$ \frac{\partial E}{\partial w_3} = 7.86 + 29.475 = 37.335. $$ Using the standard gradient descent update rule: $$ \Delta w_j = -\,\alpha \,\frac{\partial E}{\partial w_j}. $$ So explicitly: $$ \Delta w_0 = -\,\alpha \times 6.8775, $$ $$ \Delta w_1 = -\,\alpha \times 23.58, $$ $$ \Delta w_2 = -\,\alpha \times 30.4575, $$ $$ \Delta w_3 = -\,\alpha \times 37.335. $$ ## Q6 1. Feedforward (1 hidden layer, 30 nodes, KK outputs, input dimension DD): $\boxed{\text{Parameters} = (30D + 30) + (30K + K) = 30D + 30 + 31K.}$ 2. $$ (5 \times 5 \times 1) + 1 = 26 \text{ parameters}. $$ $$ 26 \times 32 = 832. $$ $$ (5 \times 5 \times 32) + 1 = 801. $$ $$ 801 \times 64 = 51{,}264. $$ $$ (3136 \times 1024) + 1024 = 3{,}212{,}288. $$ $$ (1024 \times 10) + 10 = 10{,}250. $$ $$ \begin{aligned} &\text{Conv1: } 832 \\ &\text{Conv2: } 51{,}264 \\ &\text{FC1: } 3{,}212{,}288 \\ &\text{FC2: } 10{,}250 \\ \hline &\textbf{Total: } 3{,}274{,}634. \end{aligned} $$ Thus, the CNN has: $$ \boxed{3{,}274{,}634 \text{ parameters in total}.} $$ ## Q7 1. **Task Complexity**: Larger filters capture broader context but increase computation; smaller filters learn finer details. 2. **Input Image Size**: Larger images may benefit from larger filters or bigger strides to reduce dimension quickly. 3. **Computational Constraints**: More channels and bigger filters mean more parameters and higher memory/computational cost. 4. **Depth of the Network**: Deeper networks often use smaller filters (e.g., 3×3) and fewer strides in early layers to preserve spatial information. Last modification:March 6, 2025 © Allow specification reprint Support Appreciate the author Like 如果觉得我的文章对你有用,请随意赞赏